반응형
DBSCAN (Density-Based Spatial Clustering of Application with Noise)
포인트 데이터 분석에서 DBSCAN은 항상 빠지지 않고 등장한다. 항상 무의식적으로 사용했었는데, 조금 더 자세히 알아보고 싶었다.
DBSCAN 이란?
- DBSCAN(Density-Based Spatial Clustering of Applications with Noise)은 머신 러닝에 주로 사용되는 클러스터링 알고리즘으로 Multi Dimension의 데이터를 밀도 기반으로 서로 가까운 데이터 포인트를 함께 그룹화하는 알고리즘이다.
- DBSCAN은 밀도가 다양하거나 모양이 불규칙한 클러스터가 있는 데이터와 같이 모양이 잘 정의되지 않은 데이터를 처리할 때 유용하게 사용 가능하다.
K-Means Clustering과의 차이
- 보통 Clustering 문제에서 K-Means Clustering을 우선 떠올리지만, DBSCAN이 필요한 경우도 있다.
- K-Means Clustering과 DBSCAN의 차이는 다음과 같다.
| 특징 | DBSCAN | K-means Clustering |
| Cluster의 모양 | 데이터의 Cluster 모양이 arbitrary하게 묶이는 경우 잘 Clustering 됨. | 데이터의 Cluster 모양이 Spherical한 경우에 잘 Clustering 됨. |
| Cluster의 갯수 | 군집화 갯수를 미리 정해주지 않아도 됨(밀도 기반) | 군집화될 갯수를 미리 정해줘야함 (centroid 기반) |
| Outlier | Clustering에 포함되지 않는 Outlier를 특정할 수 있음 | 모든 데이터가 하나의 Cluster에 포함됨 |
| Initial Setting | 초기 Cluster 상태가 존재하지 않음 | 초기 Centroid 설정에 따라 결과가 많이 달라짐 |
- DBSCAN과 K-means Clustering 사이에 어느 것이 좋다는 다루는 데이터에 따라 많이 달라진다.
- DBSCAN은 일반적으로 K-means Clustering에 비해 1) 불규칙 데이터를 다룰때, 2) Noise와 Outlier가 많을 것으로 예상될 때, 3) 데이터에 대한 사전 예측이 어려울때, 활용하는 것이 좋다.
- 하지만, DBSCAN은 K-means Clustering에 비해 1) Computational Cost가 많이 든다는 점, 2) 예측과 해석이 어렵다는 점의 단점이 있다.
DBSCAN 알고리즘
- DBSCAN도 2가지의 hyper parameter를 갖는다.
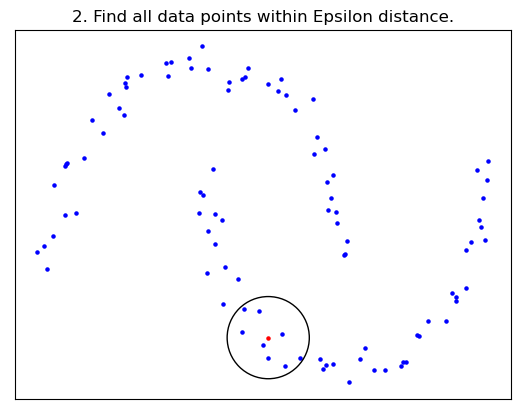
- Epsilon : Cluster를 구성하는 최소의 거리
- Min Points: Cluster를 구성 시, 필요한 최소 데이터 포인트 수
- DBSCAN의 동작 과정은 다음과 같다.
- 데이터 중, 임의의 포인트를 선택함.
- 선택한 데이터와 Epsilon 거리 내에 있는 모든 데이터 포인트를 찾음.
- 주변에 있는 데이터 포인트 갯수가 Min Points 이상이면, 해당 포인트를 중심으로 하는 Cluster를 생성한다.
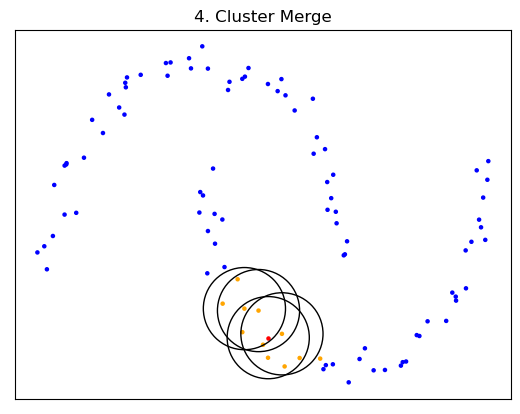
- 어떠한 포인트가 생성한 Cluster 안에 존재하는 다른 점 중, 다른 Cluster의 중심이 되는 데이터 포인트가 존재한다면 두 Cluster는 하나의 Cluster로 간주한다.
- 1~4번을 모든 포인트에 대해서 반복한다.
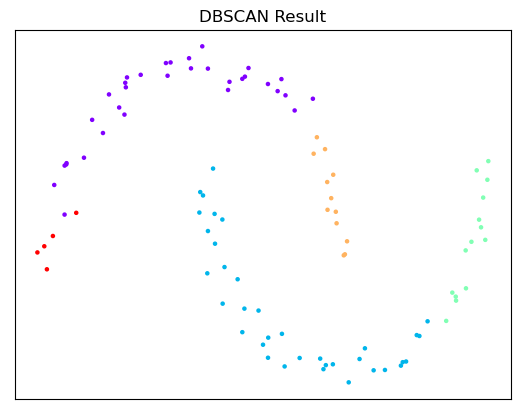
- 어느 Cluster에도 포함되지 않는 데이터 포인트는 이상치로 처리한다.



DBSCAN Python 구현
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
if __name__ == '__main__':
N = 1000
X, y = make_moons(n_samples=N, noise=0.05) # make_moons 함수를 사용
dbscan = DBSCAN(eps=0.2, min_samples=5) # DBSCAN (eps : epsilon, min_samples : min point)
dbscan.fit(X)
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_) # Clustering 결과 시각화 용도
plt.show()
'머신러닝' 카테고리의 다른 글
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
|---|---|
| Linear Regression(선형 회귀) (1) | 2023.03.23 |
| Hierarchical Clustering(계층적 군집화) (1) | 2023.03.18 |
| K-means Clustering (1) | 2023.03.13 |
| GMM(가우시안 혼합 모델) Clustering (1) | 2023.03.10 |



