K-means Clustering
K-means Clustering은 비지도 학습 기반의 Clustering 기법으로, 데이터를 Clustering하는 문제가 있으면, 가장 쉽게 연상되는 알고리즘이다. 워낙 많이 사용되어, 많이들 알고 있겠지만, K-means Clustering의 특징과 단계를 조금 더 자세히 알아보기로 한다.
K-means Clustering 이란?
- K-means Clustering은 데이터를 K개의 군집으로 나누기 위한, 거리 기반 Clustering 알고리즘이다.
- K-means Clustering은 같은 집단 내 데이터들은 비슷한 특징을 가지고 있고, 다른 집단의 데이터와는 데이터적으로 상반된 특징을 가지고 있다는 것을 가정한다. 즉, 동일 집단의 군집화를 고려하는 것 뿐만 아니라, 타집단과의 관계도 고려한다.
- K-means Clustering은 간단하고, 빠르고, 성능도 좋은 편이기 때문에 비지도 학습 기반 이미지 분류나 데이터 마이닝, 이상점 탐지등에서도 자주 활용된다.
K-means Clustering의 특징
장점
1. 간단하고, 해석이 쉽다.
- K-means Clustering 알고리즘은 거리 기반 알고리즘이기 때문에, 복잡한 연산을 포함하지 않는다. 따라서, 구현도 매우 쉬운편이고, 수행 시간도 빠르다. 또한, 거리 기반 알고리즘이기 때문에, 해석이 매우 용이하다. (같은 Cluster면, 거리가 가깝고, 다른 Cluster면 거리가 멀다.)
2. 성능이 좋다.
- Clustering 문제에서 성능이 좋다라는 기준은 애매하지만, 일반적으로 좋은 성능을 보인다.
3. 연구가 많이 되었다.
- 쉽고, 해석력이 높은 알고리즘이기 때문에, 다양한 분야에서 많이 활용 및 연구되었고, 개선되었다. 분석하고자 하는 데이터의 특성을 당장 알 수 없을때, 비슷한 분야에서 K-means Clustering 알고리즘을 활용한 연구들을 참고하기 쉽다.(중심점을 어디에 찍어야할지, 군집은 몇개로 나눌지 등등)
단점
1. 초기 값 의존도가 높다.
- 초기 값(centroid)를 어떻게 설정하냐에 따라, Clustering 결과가 매우 다르다. 특히, 초기 값이 적절하게 설정되지 않으면, Local Optimum으로 수렴되어, 초기에 원하지 않는 Clustering 모양이 될 수 있다. 이러한 문제는 분류해야하는 Cluster의 대략적인 모습을 알 수 없을때는 치명적으로 작용한다. (Local Optimum을 Global Optimum으로 착각할 수 있어서)
2. Cluster의 개수를 미리 알아야한다.
- K-means Clustering이 매우 좋은 알고리즘임에도 불구하고, 가장 큰 단점이 있다면, Cluster 개수를 미리 알아야한다는 것이라고 생각된다. 실제 데이터에서 Cluster 개수를 미리 알기 어렵기 때문에(아직 특징을 모르거나, 사전에 이론적으로 정의한 K개의 Cluster가 실제 데이터에 모두 포함되지 않을 가능성도 있기 때문에), k-mean clustering을 단독으로 사용하기 어려운 약점이 된다.
3. Cluster의 형태가 arbitrary한 경우 Clustering이 어렵다.
- Distance 기반으로 Clustering하기 때문에, 일반적으로 구형의 모양이 된다. (Euclidean 거리 사용시)
- 아래와 같이, Clustering 하고자 하는 데이터 분포가 구형 모양이 아니면, 의도한 Clustering 결과와 다르게 분류가 될 수 있다.

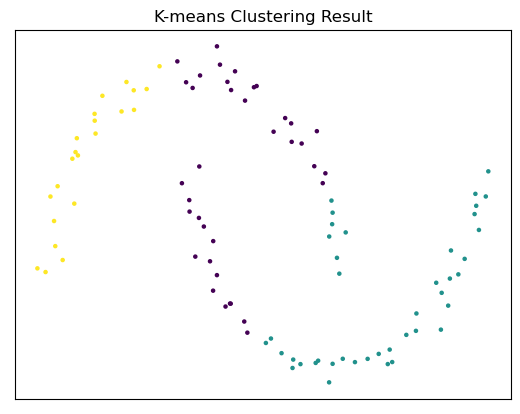
4. Outlier에 민감한 편이다.
- K-means Clustering은 Outlier에 민감한 편이다. 특히, Outlier가 centroid로 선택되면, 이상한 Clustering 결과가 될 수 있다.
전체적으로, K-means Clustering은 간단하고, 좋은 해석력과 빠른 속도, 높은 성능등을 가지고 있지만, 몇가지의 단점이 존재하여, 단점들이 개선된 알고리즘이나, Outlier 제거 등의 다른 기법들과 함께 활용된다.
K-means Clustering 알고리즘
K-means Clustering은 centroid를 설정하고, 데이터의 Cluster 할당 과정을 반복해가면서, Clustering을 수행한다.
1. 초기 centroid 설정
- K-means Clustering에서 초기의 centroid를 잡는 것은 매우 중요하다. (잘못 설정 시, Local minimum에 빠질 수 있고, 수렴 속도도 느릴 수 있다.)
- K-means Clustering의 cetroid를 설정하는 방법은 크게 3가지 방법이있다.
1) Random : 데이터 포인트 중, K개를 뽑아서, centroid로 지정한다.
2) Hierarchical clustering : Hierarchical clustering 같은 다른 clustering 방법을 사용하여, centroid에 대한 hint를 얻는다.
3) K-means++ : K-means Clustering의 초깃값을 더 효율적으로 찾기 위해, 몇가지 단계를 수행한다. (Sklean default 방법)
- 1개의 centroid를 무작위로 뽑는다.
- 데이터포인트들과 centroid 간의 거리를 계산한다.
- 각 데이터 포인트와 centroid 간 거리의 제곱을 확률로 하여, 다음 cluster의 centroid를 뽑는다. (거리가 멀수록, 다음 cluster로 뽑히는 확률이 높다는 의미)
- K개의 centroid가 만들어질때까지 반복한다.
→ 보통은 K-means++ 알고리즘을 많이 사용하지만, 계산 비용이 추가적으로 든다는 점과, 맨 처음 centroid가 이상치를 선택하게 되면, cluster 모양이 이상해진다는 점 등의 단점도 존재한다. 따라서, 데이터의 중심을 추정이 가능하다면, 직접 설정하는 것도 좋은 방법이다.
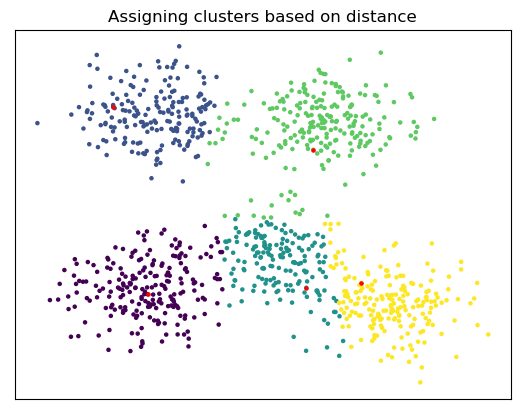
2. 각 데이터 포인트와 centroid 거리 측정 & Cluster 할당
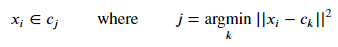
- K-means Clustering의 수식은 위와 같다. 즉, K개의 centroid 들 중, 현재 point와 거리가 가장 가까운 centroid가 형성하는 cluster에 데이터가 포함한다.
- 거리를 구하는 방법은 지정하기 나름이지만, 보통 유클리디안 거리를 사용한다.
3. centroid 업데이트

- 새로운 centroid로는 2번에서 할당한 cluster들의 평균 값을 활용한다.
- 새로운 centroid는 2번에 할당된 cluster의 중간으로 이동할 것이다.
4. 2~3 단계를 반복
- 수렴할때까지, cluster 할당, centroid 업데이트를 반복한다.




K-means Clustering Python 구현
- scikit-learn의 KMeans를 사용하면 쉽게 사용 가능하다.
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
if __name__ == '__main__':
X, y = make_blobs(n_samples=1000, centers=5, random_state=10, cluster_std=2) # 데이터 생성
kmeans = KMeans(n_clusters=5, init=rand_array, n_init=1, max_iter=100)
kmeans.fit(X)
kmeans.labels_ # 학습에 활용된 데이터의 cluster를 예측
kmeans.predict(X) # 임의의 point가 어느 cluster에 포함되는지 예측
kmenas.transform(X) # 임의의 point와 할당된 cluster의 centroid 간의 거리를 구함- n_clusters : 클러스터 개수 (*hyper-parameter)
- init : 초깃값 설정 방법, 'k-means++', 'random', numpy_array(centroid를 직접 지정해줄 때) ,default는 k-means+
- max_iter : 2~3 단계 최대 반복 횟수 (default:300)
- random_state : k-means++ 등에서 무작위성을 제어하기 위한 시드 값, 재현을 위해 설정이 필요함
- algorithm : k-means clustering 데이터 계산 시, 어떤 알고리즘을 사용할 것인지, 'auto', 'full', 'elkan'이 있다. full은 모든 데이터를 2~3 단계에서 활용하는 것이고, elkan은 데이터 연산 부하를 줄이기 위해, 불필요한 연산을 줄이는 방법이다. auto는 데이터 크기와 특징에 따라, 자동으로 설정해줌
- metric : 거리 측정 방식, 'euclidean', 'manhattan', 'cosine', 'l1', 'l2', 'manhattan_l1', 'manhattan_l2' 등이 있음 (default : euclidean, 사용자 지정 함수도 활용 가능)
'머신러닝' 카테고리의 다른 글
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
|---|---|
| Linear Regression(선형 회귀) (1) | 2023.03.23 |
| Hierarchical Clustering(계층적 군집화) (1) | 2023.03.18 |
| GMM(가우시안 혼합 모델) Clustering (1) | 2023.03.10 |
| DBSCAN(밀도 기반 클러스터링) (5) | 2023.03.08 |



