반응형
GMM (Gaussian Mixture Model) Clustering
GMM Clustering은 Clustering 문제에서 각 Cluster에 포함될 확률이 포함될 때, 자주 사용하는 알고리즘이다. 대략적인 컨셉만 알고 쓰고 있지만, 조금 더 자세히 알아보고 싶었다.
GMM 이란?
- GMM(Gaussian Mixture Model) Clustering은 어떠한 데이터 분포가 여러 개의 Gaussian 분포 여러 개가 섞여서 만들어졌다고 생각하고, 해당 데이터 분포를 이루는 여러 개의 Gaussian 분포로 나타내는 확률적 생성 모델이다.
- GMM Clustering은 다른 Clustering 모델과 달리, 해당 Cluster에 속할 확률을 같이 나타내주기 때문에, Clustering 결과에 불확실성도 함께 고려할 수 있다.
- GMM Clustering은 확률을 포함한 Clustering이나, 데이터 생성, 이상치 탐지(다른 이상치 제거 알고리즘과 함께 사용되는 경우) 등에 유용하게 사용된다.
GMM Clustering, K-Means Clustering, DBSCAN과의 차이
- 보통 GMM Clustering을 단독으로 사용하지는 않지만, (초기값 설정에서 다른 Clustering 알고리즘의 도움을 많이 받음), 같은 Clustering 알고리즘이라는 점에서 DBSCAN과 K-means Clustering과 비교해 보기로 한다.
| 특징 | GMM Clustering | DBSCAN | K-means Clustering |
| Cluster의 모양 | 데이터의 Cluster 모양이 Gaussian 분포를 따르는 것을 가정 | 데이터의 Cluster 모양이 arbitrary하게 묶이는 경우 잘 Clustering 됨. (비선형 구조) | 데이터의 Cluster 모양이 Spherical한 경우에 잘 Clustering 됨. (비선형 구조) |
| Cluster의 갯수 | .군집화될 갯수를 미리 정해줘야 함 | 군집화 갯수를 미리 정해주지 않아도 됨(밀도 기반) | 군집화될 갯수를 미리 정해줘야함 (centroid 기반) |
| Outlier | 데이터를 Gaussian 분로 가정하기 때문에, 잘못된 모델링이 될 수 있음 (Outlier에 취약함) | Clustering에 포함되지 않는 Outlier를 특정할 수 있음 | 모든 데이터가 하나의 Cluster에 포함됨 |
| Initial Setting | 초기 군집 중심, 초기 공분산 행렬에 따라 결과가 많이 달라짐 | 초기 Cluster 상태가 존재하지 않음 | 초기 Centroid 설정에 따라 결과가 많이 달라짐 |
| Computing Cost | 높음 (EM 알고리즘) | 낮음 (K-means Clustering보다는 높음) | 낮음 |
| Cluster 속할 확률 | Gaussian 다변수 정규 분포를 사용하여, 각 Cluster 포함될 확률을 계산 가능 | 밀도 기반으로 간접 추정 | 거리 기반으로 간접 추정 |
GMM Clustering 원리
- GMM Clustering 알고리즘은 데이터 분포를 여러개의 Gaussian 분포들의 합 들이 혼합된 상태로 구성되어 있다고 가정하기 때문에, 데이터는 아래 수식과 같이 모델링 된다.

- 𝑝(𝑥) : 데이터 포인트 x의 확률
- 𝜙𝑖 : i 번째 Gaussian 분포의 합의 weight (weight의 합은 1)
- N(𝑥|𝜇𝑖,Σ𝑖) : i번째 Gaussian 분포의 확률 밀도 함수
- 𝜇𝑖 : i번째 Gaussian 분포의 평균
- Σ𝑖 : i번째 Gaussian 분포의 공분산 행렬
- GMM Clustering 알고리즘은 결국 GMM 수식에서 𝜙𝑖(각 Gaussian 분포의 weight), 𝜇𝑖 (각 Gaussian 분포의 평균), Σ𝑖 (각 Gaussian 분포의 공분산 행렬)을 찾는 과정이다.
- 이를 위해, EM (Expectation & Maximization) 알고리즘을 사용한다. EM 알고리즘은 Expectation step과 Maximization Step으로 나뉜다.
- E-step (Expectation step) :
- 각 데이터 포인트가 어떤 Gaussian 분포에 속하는지에 대한 확률을 추정한다.
- M-step (Maximization step)
- E-step에서 추정된 확률을 이용해서, Gaussian 분포의 Parameter(weight, 평균, 공분산 행렬)를 업데이트한다.
- 이때, 업데이트를 위한 목적함수는 log-likelihood 함수를 이용한다.
- log-likelihood 함수가 최대화하는 방향으로 Parameter를 업데이트한다. (어떠한 data point가 어떤 Gaussian 분포에 포함될 확률이 높도록 학습. 즉, 모든 데이터 포인트가 어떠한 Gaussian 분포에 포함될 확률이 높도록 parameter를 업데이트)
- E-step (Expectation step) :





- 다만, GMM은 초기값 설정에 매우 민감하다. 만약 inital mean 값이 잘못 찍혔을 때, Clustering의 결과가 원하는 바와 다르게 나올 수 있다.


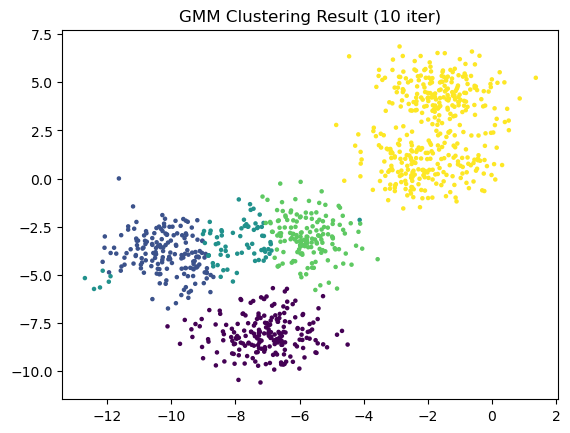
- 따라서, GMM Clustering을 단독으로 사용하기 보다는 K-means Clustering 등을 이용하여, Initial 값들을 setting 한다. (scikit-learn의 GaussianMixture 함수도 초깃값의 default 설정이 k-means 방법을 통해 구하는 것으로 되어있다.)
GMM Clustering Python 구현
- scikit-learn의 GaussianMixture 함수를 사용하면 쉽게 사용 가능하다.
import numpy as np
from sklearn.datasets import make_blobs # Clustering 데이터 생성을 위해
from sklearn.mixture import GaussianMixture
if __name__ == '__main__':
X, y = make_blobs(n_samples=1000, centers=5, random_state=1) # Sample 데이터 생성
gmm = GaussianMixture(n_components=5, random_state=42, n_init=10)
gmm.fit(X)
gmm.means_ #gmm의 mean 값들을 확인 가능
gmm.weights_ #gmm의 weight 값들을 확인 가능
gmm.covariances_ #gmm의 공분산 행렬 확인 가능
gmm.predict(X) #각 point가 어느 Cluster에 포함되는지 결과를 확인
gmm.predict_proba(X) #각 point가 각 Cluster에 포함될 확률 (point 당 n_components개 만큼)
'머신러닝' 카테고리의 다른 글
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
|---|---|
| Linear Regression(선형 회귀) (1) | 2023.03.23 |
| Hierarchical Clustering(계층적 군집화) (1) | 2023.03.18 |
| K-means Clustering (1) | 2023.03.13 |
| DBSCAN(밀도 기반 클러스터링) (5) | 2023.03.08 |



