반응형
Linear Regression
Linear Regression 모델은 매우 간단하고, 직관적이여서, 머신러닝하면 가장 대표적으로 생각나는 모델이다. 딥러닝 관련 책들에 항상 1장으로 등장했을만큼, 기초적이고 매우 중요하다.
Linear Regression 이란?
- Linear Regression은 어떠한 독립 변수들과 종속 변수 간의 관계를 예측할때, 그 사이 관계를 선형 관계(1차 함수)로 가정하고, 모델링하는 지도 학습 알고리즘이다.
- Linear Regression은 보통, 인자와 결과 간의 대략적인 관계 해석이나, 예측에 활용된다.
- Linear Regression은 확률 변수를 수학적 함수의 결과인 변수(모델링 결과값)으로 연결해준다는데, 그 의미가 크다.
- Linear Regression은 변수의 수에 따라, 다음과 같이 구분된다.
- 변수 1개와 종속 변수 간의 선형 관계 모델링은 단순 선형 회귀 분석이라고 한다.
- 독립 변수 여러 개와 종속 변수 간의 선형 관계 모델링은 다중 선형 회귀 분석이라고 한다.
→ 단순 선형 회귀 분석은 Visualization이 쉽고(2차원 공간에서 선형 함수로 표현 가능), 변수가 하나여서 이해가 쉽지만, 실생활에서의 문제들은 보통 다중 선형 회귀 문제인 경우가 많다.

y: 종속 변수, βk :회귀 계수, Xk:독립 변수, ε: 오차항(모델으로 설명할 수 없는 부분), X1까지만 존재하면, 단순 선형 회귀 분석

Linear Regression의 Residual(잔차)
- 앞서 말한대로, Linear Regression에서 종속 변수는 관찰의 결과인 확률변수이기 때문에, 오차(error)를 포함한다.
- 오차를 알기 위해서는, 모델링을 위한 인자와 종속 변수 간의 모든 경우의 수를 학습해야하지만, 현실적으로 불가능하다.
- 따라서, Linear Regression에서는 오차를 사용하지 않고, 표본집단(학습데이터)으로 학습된 모델의 예측값과 실제 관측값 사이의 차이인 잔차(residual) 개념을 사용한다

- .Linear Regression은 i.i.d 라는 가정을 따른다.
- 정규성 가정 : 잔차는 정규 분포를 따른다고 가정한다. 잔차가 정규 분포를 따르지 않고, 특정한 분포를 따른다면, 회귀 모델의 예측값을 신뢰하기 어렵다.
- 확인 방법 : 잔차 분포도 Visualization 확인, 잔차 정규성 검정
- 등분산성 가정 : 잔차의 분산은 일정하다.
- 확인 방법 : 잔차-예측값 산포도 확인,
- 독립성 가정 : 모든 잔차들은 서로 독립적이다. 만약, 잔차 간의 상관 관계가 있다면, 추정된 회귀식에서 설명하지 못하는 다른 어떠한 관계가 존재할 수 있다.
- 확인 방법 : 잔차의 자기상관 함수 확인
- 정규성 가정 : 잔차는 정규 분포를 따른다고 가정한다. 잔차가 정규 분포를 따르지 않고, 특정한 분포를 따른다면, 회귀 모델의 예측값을 신뢰하기 어렵다.
Linear Regression의 학습
- Linear Regression의 학습 목적은 종속 변수와 설명 변수 간의 관계를 가장 잘 나타낼 수 있는 선형식을 모델링하는 것이다.
- Linear Regression의 모델 추정을 위해서, 보통 예측값과 실제관측값인 잔차의 제곱을 최소화하는 최소제곱법(OLS)을 사용한다.

y_i : i번째 데이터의 실제 종속 변수 값, ŷ_i 데이터의 예측값
- 최소제곱법을 활용하는 이유는 다음과 같다.
- 잔차의 제곱은 항상 양수이기 때문에
- 잔차의 제곱은 큰 오차를 더욱 강조가 가능하기 때문에
- 잔차의 제곱은 미분이 가능하기 때문
- 단순 선형 회귀 분석에서는 최소제곱법을 이용하여, 회귀계수를 다음과 같이 추정할 수 있다.


- 다중 선형 회귀 분석에서는 최소제곱법을 이용하여, 회귀 계수 행렬을 다음과 같이 추정할 수 있다.



Linear Regression의 평가
- Linear Regression을 평가하기 위해서, 결정 계수(coefficient of determination) 개념을 활용한다.
- 결정 계수는 회귀 분석에서 모델이 얼마나, 실제 데이터를 잘 예측하는지를 나타내는 지표이다.
- 결정 계수를 구하기 위해서, 세가지 값의 의미 알아야한다.
- SST (Total Sum of Squares): 종속 변수 y와 그 평균값 ȳ 간의 차이를 제곱하여 모두 더한 값
- SSR (Residual Sum of Squares) : 종속변수 y에서 모델 추정값 간 차이를 제곱하여 모두 더한 . (잔차의 총합)

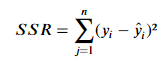

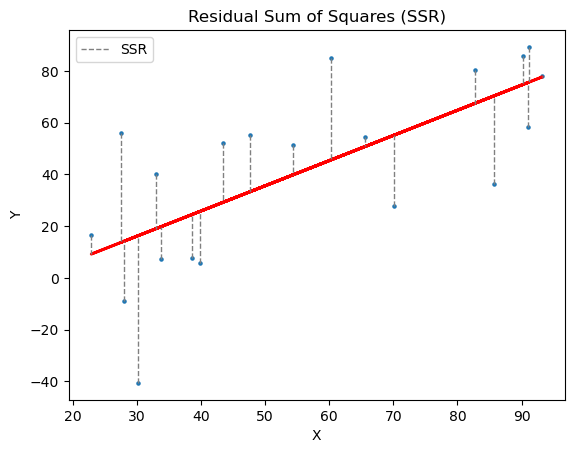
- 결정 계수는 SST와 SSR을 통해 아래와 같은 식으로 구한다.
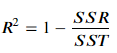
- 결정 계수는 전체 오류(분산 개념) 중, 모델로 설명 가능한 오류의 범위의 비중을 뺀 비중으로, 1에 가까울수룩 일반적으로 예측력이 좋다고 해석한다.
- 결정 계수가 대략적인 모델의 적합성을 파악할 수 있지만, 절대적인 지표는 아니다.
Linear Regression의 Python 구현
- Linear Regression은 scikit-learn의 linear_model의 LinearRegression을 통해 쉽게 사용 가능하다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
if __name__ == '__main__':
# 테스트용 데이터 생성
x = np.random.rand(1000)*100
y = 0.8*x+np.random.randn(1000)*30
# Linear Regrssion model 생성
model = LinearRegression()
# Linear Regression model 학습
model.fit(x.reshape(-1,1), y)
# Prediction
y_new = model.predict(np.array([6]).reshape((-1, 1)))
print("Data Prediction: ", y_new)
# Linear Regression model 평가
r_sq = model.score(x.reshape(-1,1), y)
print("결정 계수: ", r_sq)
# Linear Model 식
b0,b1 = model.intercept_, model.coef_[0]
print("b0",b0)
print("b1",b1)
# 시각화
plt.scatter(x, y, s=5)
plt.plot(x, model.predict(x.reshape(-1,1)), color='red', linewidth=2)
plt.annotate('y = '+str(round(b1,2))+'x '+str(round(b0,2)), xy=(100, 100), xytext=(80, 80))
plt.show()'머신러닝' 카테고리의 다른 글
| Logistic Regression(로지스틱 회귀 분석(2)-다중 분류) (1) | 2023.04.23 |
|---|---|
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
| Hierarchical Clustering(계층적 군집화) (1) | 2023.03.18 |
| K-means Clustering (1) | 2023.03.13 |
| GMM(가우시안 혼합 모델) Clustering (1) | 2023.03.10 |



