반응형
Logistic Regression
Logistic Regression의 원리는 이진분류에서 다뤘다. 하지만, 실제 데이터 분석 시에는 이진 분류보다는 다중 클래스 사이에서 데이터가 어느 클래스에 속하는지를 분류하는 문제가 많다. 사실 다중 분류를 위한 로지스틱 회귀는 이진 분류와 내용 차이가 크게 없지만, 많이 사용하는 만큼 따로 나눠서 소개를 하고 한다.
다중 Logistic Regression 이란?
- 3개 이상의 클래스 중, 하나의 클래스에 속하는지를 예측하는 문제이다.
- 이진 분류와 가장 다른 점은, 이진 분류는 분류 문제의 정답이 '참'일 확률(p)만 고려하여, '참'과 '참이 아님'을 분류하면 되지만, 다중 분류는 여러 가지 클래스 중, 예측 모델이 속할 확률이 가장 높은 클래스를 찾는 문제이다.
- 즉, 정답이 이진 분류에서는 정답 예측을 한 차원('참'일 확률 p)에서만 끝낼 수 있었지만, 다중 분류의 예측은 클래스의 개수만큼의 예측 결과가 필요하다.
- 이러한 다중 분류를 위해 다중 로지스틱 회귀 모델에서는 일반적으로 Softmax 함수를 사용한다.
※ Softmax 함수
- K개의 클래스가 있는 다중 분류 문제에서 j번째 softmax 함수 결과는 아래와 같이 나타난다.

- Softmax 함수는 Logistic 함수의 일반화된 형태이다.
- Softmax 함수는 각 클래스에 속할 확률(p)을 각 클래스들에 속할 확률들의 합으로 나눠서, 0부터 1 사이로 Normalization 한 형태이다.
- 일반적으로 Softmax 함숫값이 가장 큰 클래스로 예측 모델의 결과를 낸다.
다중 Logistic Regression의 학습 방법
- 다중 Logistic Regression의 학습을 위해서도 최대우도방법(MLE, Maximum Likelihood Estimation)을 사용한다.
- 다중 Logistic Regression의 학습을 위해서, 학습에 사용되는 정답을 One-hot vector 형식으로 나타내야 한다.
- 다중 Logistic Regression의 학습을 위해서는 일반적으로 크로스 엔트로피(Cross Entropy) 함수를 사용하여, 목적 함수를 정의한다.
[크로스 엔트로피]
- 크로스 엔트로피는 정보 이론에서 사용되는 개념으로, 두 확률 분포가 얼마나 다른지를 측정하는 방법이다.
- 크로스 엔트로피 식은 다음과 같다.

p: 실제 확률, q: 예측 확률, n: 분포의 원소 개수
- 크로스 엔트로피의 그래프를 확인해 보면, 예측 확률 q가 실제 확률 p과 동일한 지점에서 최솟값을 나타냄을 확인할 수 있다.
- 즉, 크로스 엔트로피가 최솟값을 가지는 구간이 실제 확률과 가장 비슷한 예측을 하였다고 할 수 있다.
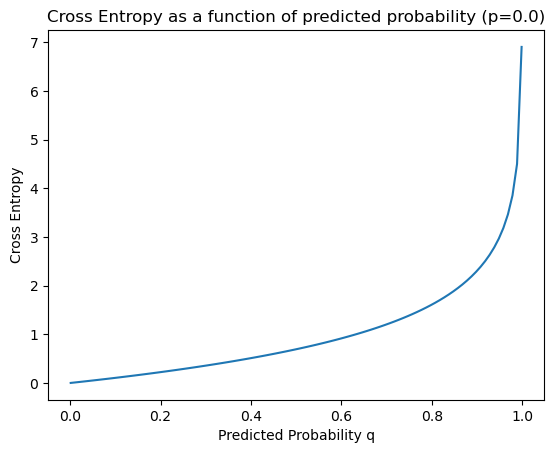

- 분류 문제에는 종속 변수가 범주형(각 클래스에 속할 확률이 0 or 1)으로 나타나기 때문에(One-Hot vector), 첫 번째 그래프처럼 실제 분포를 정확히 예측하였을 때, '0' 값을 갖는다.
[One-Hot Vector]
- One-Hot vector는 범주형 데이터를 다루기 위해, 사용되는 벡터 표현 방법이다.
- 클래스에 정수형 범주를 붙인다면, 클래스 간의 대소 관계와 순서가 모델의 학습과정에서 고려되어, 숫자형 범주 자체를 '중요도'로 오해하여 학습될 수 있다. 이를 막기 위해 One-Hot vector를 이용하여 정답 레이블을 표시한다.
- K개의 클래스가 있는 범주형 데이터가 있는 분류 문제에서, 해당 데이터가 실제로 i번째 클래스에 속해있다고 하면, i번째 데이터를 제외한 K-1개 클래스는 0으로, i번째 클래스는 1의 값을 갖는다.
- One-Hot vector는 해당 클래스에 속할 확률을 나타낸다고 생각할 수 있다.
[다중 로지스틱 회귀 목적함수]
- 다중 로지스틱 회귀를 이용한 분류 문제의 목적은 실제 데이터가 속한 클래스와 비슷한 분포를 예측하는 모델을 만드는 것이다.
- 위의 크로스 엔트로피 식에서 p를 실제 데이터의 분포를 One-Hot vector로 변환한 값, q를 모델이 예측한 분포라고하면, 크로스 엔트로피 값이 최소인 지점이 모델이 실제 데이터를 가장 잘 예측하였을 때라고 생각할 수 있다.
- 결국 다중 로지스틱 회귀 모델의 학습의 목적은 Softmax 함수의 형태로 구해진 예측 모델의 결과가 실제 정답의 분포에 가장 유사한 형태를 갖도록, 크로스 엔트로피 값을 최소화할 수 있는 모델 파라미터를 찾는 것이다.

y : 실제 정답 레이블(one-hot vector 형태), K: 클래스 개수, N: 데이터 개수
- 다중 로지스틱 회귀 목적함수는 다음과 같다.

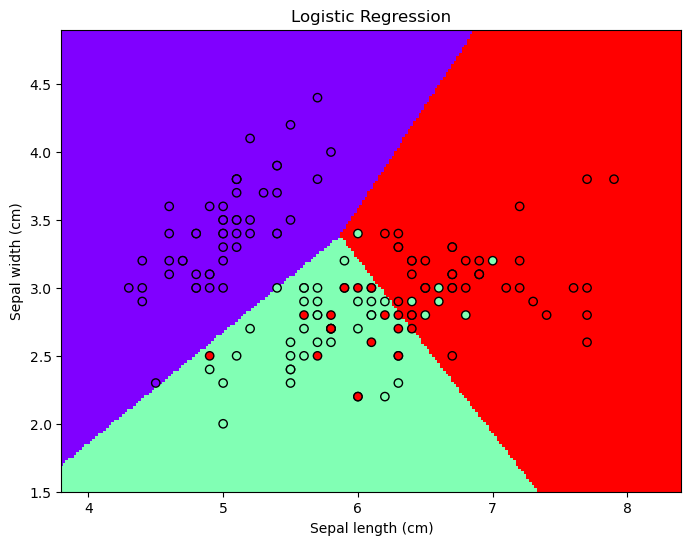
Logistic Regression의 Python 구현
- 다중 Logistic Regression은 Python의 Sklearn을 이용하여 쉽게 구현 가능하다.
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
if __name__ == "__main__":
# 데이터 Load (iris 데이터 사용, X :꽃의 길이와 너비, y: 꽃의 종류, 3개의 class)
iris = load_iris()
X = iris.data[:, :2]
y = iris.target
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)
# 모델 학습
clf = LogisticRegression(random_state=1)
clf.fit(X_train, y_train)
# 모델 예측
y_pred = clf.predict(X_test)
# 정확도 계산
acc = accuracy_score(y_test, y_pred)
print("Accuracy:", acc)
'머신러닝' 카테고리의 다른 글
| Decision Tree(의사결정나무 ) (17) | 2023.08.29 |
|---|---|
| t-SNE(t-distributed Stochastic Neighbor Embedding) (1) | 2023.04.26 |
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
| Linear Regression(선형 회귀) (1) | 2023.03.23 |
| Hierarchical Clustering(계층적 군집화) (1) | 2023.03.18 |



