t-SNE는 딥러닝 모델에서 feature의 유사도를 파악하기 위해 시각화할 때, 정말 많이 사용했던 방법이다. 단순 차원축소를 해주는 알고리즘이다라고만 이해하고 있었는데, 이번 기회에 완벽히 이해해보고자 한다.
t-SNE 이란?
- t-SNE(t-distributed Stochastic Neighbor Embedding)는 고차원 데이터를 저차원 영역으로 표현하기 위한 비선형 차원 축소 기법이다.
- 여러 Feature 들의 차원 중에서 의미가 큰 차원을 선택하는 Feature Selection과 달리, 고차원 데이터의 구조와 패턴을 유지하면서, 차원 축소를 가능하게 한다.
- 딥러닝 등의 중간 Layer의 Output Feature 들은 대체적으로 고차원의 영역의 데이터이다. 이러한 데이터들은 직관적으로 이해하기가 어렵기 때문에, 저차원으로 시각화하여 Visualization을 진행하는데, t-SNE가 자주 사용된다.
- PCA(주성분 분석)과 차원축소의 개념에서는 비슷하지만, 목적과 방식이 달라, 혼용해서 보완 사용하기도 한다.
| t-SNE | PCA | |
| 목적 | 고차원 데이터를 저차원으로 바꿔, 시각화 (유사한 데이터는 가깝게, 다른 데이터는 멀게) |
고차원 데이터를 저차원으로 바꿔, 데이터의 구조와 패턴을 파악 |
| 방법 | 확률 분포를 이용하여 고차원 데이터와 저차원 데이터 간의 유사도를 계산하고, 최적화함. | 데이터의 분산을 최대한 보존하는 축을 찾아서 차원을 축소함 (고유값 분해) |
| 알맞은 데이터 유형 |
선형적 & 비선형적 데이터 모두 (데이터 간 유사도가 극명하면 유리) | 데이터가 선형적으로 구성되어 있는 경우 |
| 주의점 | 저차원에서의 유사도 최적화 과정이 포함되어서, PCA보다 computation cost가 높음 최적화 과정이 있기 때문에, 데이터셋 구성에 따라 결과가 달라짐 |
비선형적 데이터에 대해서는 성능이 떨어짐 |
t-SNE 알고리즘
- t-SNE의 원리는 쉽게 말해서, 고차원 공간에서 가까운 것은 저차원에서도 가깝게, 고차원에서 먼 것은 저차원에서도 멀게 유지하는 것이다.
- 기본적으로 t-SNE는 고차원 데이터 포인트들간 유클리디안 거리를 이용해서, 유사도를 조건부 확률로 바꿔서, 유사도를 나타내겠다는 SNE를 개선한 방법이다.
- SNE의 유사도를 조건부 확률로 바꾸는 것이 처음에 잘 이해가 안 되는데, 쉽게 생각하면, Gaussian 분포의 PDF를 생각하면 된다. 이 식에서 평균이 데이터 포인트 i라고 하면, 평균이 i 포인트인 Gaussian 분포를 생각하면 된다. 즉, 한 데이터 포인트를 중심으로 다른 데이터 포인트 간의 거리는 정규 분포를 따른다고 생각하면 된다.
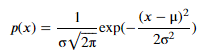
- 우선, t-SNE를 이해하기 위해 SNE 원리를 이해해보자.
[SNE 원리]
1. 각 데이터 포인트간 Euclidean Distance를 구한다.

2. 두 데이터 포인트 간 거리를 d라고 했을때, 두 데이터 포인트 사이의 거리가 d 일 확률은 다음과 같은 정규분포의 조건부 확률로 나타난다. 즉, 거리를 다음과 같이 나타낸다. (p(i|j)와 p(j|i)가 다르다는 점을 주목해야한다.)
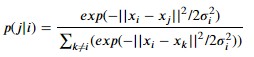
3. SNE의 원리는 고차원의 거리를 그대로 유지하는 저차원에서의 모델을 찾는 것이다. 저차원에서 σ의 제곱(분산)이 1/2 값을 갖는 분포를 가정하면, 저차원에서 데이터 분포 간의 거리는 다음과 같이 나타낼 수 있다.
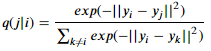
4. 학습의 목적은 고차원에서 데이터 포인트간의 거리를 나타내는 분포 p를 제일 잘 표현할 수 있는 저차원의 근사분포 q를 찾는 것이다. q가 p와 비슷한 분포가 되기 위해, 두 분포간의 KL(Kullback-Leibler) Divergence가 작아지도록 학습한다. (Gradient Descent를 이용, 두 분포가 완전히 같아졌을때, KL divergence는 0)
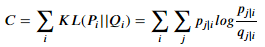
- SNE도 좋은 방법이지만, t-SNE는 SNE보다 다음과 같은 면을 수정했다.
1. 비대칭성 → 대칭성
조건부 확률 기반에서, 고차원의 두 데이터 포인트 i와 j 사이의 거리인 p(i|j)와 p(j|i)는 다르다.(Sigma가 다르다) t-SNE에서는 둘 사이의 거리를 정의하는 확률을 아래와 같이 수정하여 대칭성을 부여하였다. (이로 인해, 최적화 속도가 빨라졌다. → 어느 방향에서도 동일하게 수렴 가능하기 때문에 안정적이다.)

2. Gaussian 분포 → t-분포
고차원을 저차원으로 축소하다 보면, 고차원에서 데이터가 많이 분포하는 구간에서 축소된 데이터들은 서로 많이 뭉치게 된다. 10차원에서 봤을 때는 다양한 값들을 가진 데이터들이 2차원으로 차원 축소가 되면, 거의 비슷하게 보일 수 있다. (RGB 이미지에서 구분 잘되던, 그림들이 흑백에서 구분이 잘 안 되는 걸 생각하면 된다.) 이를 완화하기 위해서는 데이터의 분포가 고르게 퍼져있는 구조가 유리하다. t-SNE에서는 거리 분포를 Gaussian 분포 대신에 t 분포를 도입하여, 데이터를 퍼뜨렸다.


v: 자유도, B : 베타 함수

[t-SNE]
1. 각 데이터 포인트간 Euclidean Distance를 구한다.

2. 두 데이터 포인트 사이의 거리가d일 확률은 다음과 같은 조건부 확률로 나타난다. 다만, 앞에 말했던 대로, 대칭성 확보를 위해 두 데이터 포인트 사이의 거리를 다음과 같이 정의한다. (고차원의 거리 분포는 Gaussian 분포를 그대로 유지한다.)
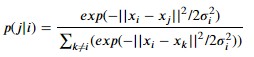

3. t-SNE는 SNE와 달리, 저차원에서 분포를 t-분포로 가정한다. 따라서, 데이터 포인트 간 거리를 다음과 같이 나타낼 수 있다. (일반적으로 자유도가 1인 t-분포를 사용한다.)

4. t-SNE도 마찬가지로, 학습의 목적은 고차원에서 데이터 포인트 간의 거리를 나타내는 분포 p를 제일 잘 표현할 수 있는 저차원의 근사분포 q를 찾는 것이다. q가 p와 비슷한 분포가 되기 위해, 두 분포간의 KL Divergence가 작아지도록 학습한다. (Gradient Descent를 이용)
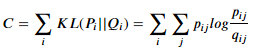
t-SNE 파이썬 구현
- scikit-learn의 TSNE를 사용하면, 쉽게 TSNE를 사용 가능하다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.manifold import TSNE
if __name__ == '__main__':
# Data Load (MNIST: 64 dim)
digits = datasets.load_digits()
X = digits.data
y = digits.target
# t-SNE(64 to 2)
tsne = TSNE(n_components=2, random_state=1)
X_tsne = tsne.fit_transform(X)
# t-SNE Visualization
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y)
plt.show()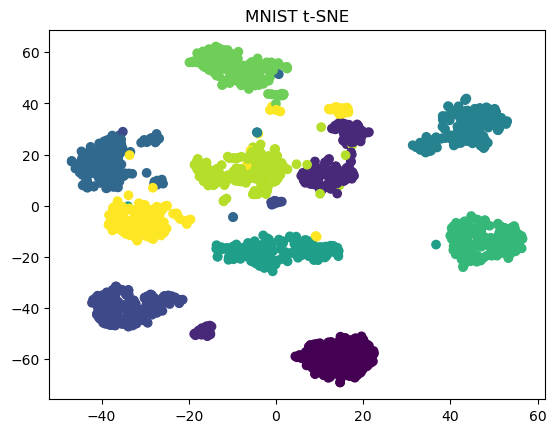
'머신러닝' 카테고리의 다른 글
| Batch Normalization (Accelerating DeepNetwork Training by Reducing Internal Covariate Shift) 논문 리뷰 (43) | 2023.11.10 |
|---|---|
| Decision Tree(의사결정나무 ) (17) | 2023.08.29 |
| Logistic Regression(로지스틱 회귀 분석(2)-다중 분류) (1) | 2023.04.23 |
| Logistic Regression(로지스틱 회귀 분석(1)-이진 분류) (1) | 2023.04.17 |
| Linear Regression(선형 회귀) (1) | 2023.03.23 |



