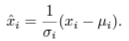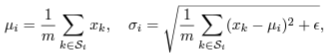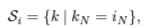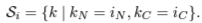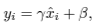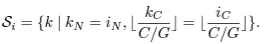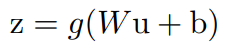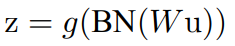Layer Normalization 배경 설명
- Layer Normalization은 토론토 대학에서 2016년 발표한 논문이다. Geoffrey E. Hinton이 저자로 포함되어 있다.
- CNN에서 BN이 주목을 받게 되면서, RNN에 적용 가능한 LN을 소개하였다.
- BN의 단점을 극복하는 것(RNN에 적용이 안된다는 점)이 논문의 시작이기 때문에 BN에 대해 먼저 알아야 한다.
Batch Normalization (Accelerating DeepNetwork Training by Reducing Internal Covariate Shift) 논문 리뷰
항상 문제에 봉착하기 전에는 내가 모르는 것이 뭐인지 모르게 된다. 항상 Batch Normalization은 당연하게 사용하였지, 그 의미에 대해서 대략적으로만 알고 있었던 것 같아서, 이번 기회에 Batch Normal
devhwi.tistory.com
- 최근 유행하는 Transformer에 normalization 방법으로 거의 무조건 사용되기 때문에, 매우 중요한 논문이다.
Abstract
- 딥러닝 학습을 위한 연산은 비용이 크다.
- 이러한, 학습 시간을 줄이기 위한 방법으로 중간 layer의 결과들을 normalize 하는 방법이 있다.
- 최근에는 mini batch 내에서 mean과 variance를 이용하여 normalization 방법인 Batch Normalization(BN)이 널리 사용되고 있다. 이 방법은 학습 시간을 크게 줄여준다.
- 하지만, BN은 mini-batch 크기에 의존적이고, recurrent neural network에 적용 방법이 명확하지 않다.
- 이 논문에서는 하나의 training 데이터 내에서 한 layer의 mean과 variance를 이용하여 normalization 하는 "Layer Normalization(LN)"을 소개한다.
- BN처럼 normalization 후, activation 적용 전에 적용되는 bias와 gain을 이용한다.
- BN과 다르게 LN은 training과 test time의 normalization 방법이 같다.
- 또한, LN은 각 time step에 따른 dependency가 없기 때문에, recurrent model에도 적용 가능하다.
Introduction
[배경 - Batch Normalization]
- 딥러닝 학습이 점점 발전하고 있지만, 학습에 매우 긴 시간이 소요된다.
- 딥러닝 학습 속도를 향상하기 위해, 여러 머신을 사용한 병렬처리 등 여러 방법이 등장하고 있다.
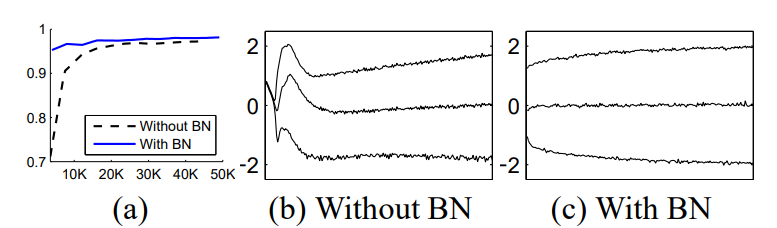
- 그중 BN은 training data에 mean과 standard deviation을 이용한 normalization 방법을 적용하여, 학습 속도를 향상했다.
[BN의 문제]
- BN은 고정된 depth의 network에서 직관적이고 효과적이다. 하지만, RNN과 같은 길이가 달라지는 network에서는 time step마다 statistics가 달라지기 때문에 BN을 적용하기 어렵다.
- 또한, BN은 batch size가 작은 경우에는 효과적이지 않았다.
[LN]
- 이 논문에서는 layer normalization이라는 간단하게 학습속도를 향상할 수 있는 normalization 방법을 소개한다.
- BN과 다르게 summed input(residual connection이 더해진 값들 or RNN처럼 누적된 값들) 내에서 normalization을 진행하기 때문에, training set 들간의 의존성을 가지지 않는다.
- LN을 사용하여 RNN에서 속도와 성능이 빨라진 것을 보인다.
Layer Normalization
- BN의 단점을 극복하기 위한, LN을 소개한다.
- "covariate shift" 문제를 해결하기 위해, 각 layer의 mean과 variance를 이용한 normalization을 진행한다. 이를 위해, mean과 standart deviation을 아래와 같이 정의한다. (H : hidden unit 수)

- 이렇게, mean과 shift를 정의하여 BN과 달라진 점은 LN에서는 동일 layer들이 동일 통계값을 보고, training set 들 간에는 서로 의존성이 존재하지 않는 것이다.
- LN은 training set 간 의존성이 없기 때문에, batch size에 영향을 받지 않는다. (1도 가능하다.)
Layer normalized recurrent neural networks
- NLP에서는 training set마다 다른 길이를 가지는 경우가 흔하다. 이것은 RNN이 각 time-step마다 동일 weight를 공유하기 때문이다.
- 하지만, BN을 RNN에 적용하려 할 때, 문제가 발생한다. 각 time step마다 별개의 statistics를 저장해 놔야 하기 때문이다. 특히, test set의 sequence 길이가 training set보다 길 때는 문제가 생긴다. (통계값이 없기 때문에)
- LN은 현재 time-step의 input에서만 normalization을 진행하기 때문에, 이러한 문제가 발생하지 않는다. 또한, 모든 time step에서 공유 가능한 하나의 셋의 gain과 bias를 가진다.
- RNN에서 LN을 위한 statistics는 다음과 같이 구해진다. (⊙: element-wise multiplication, b: bias, g: gain)
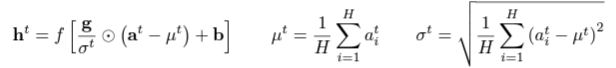
- RNN이 LN을 적용하면, 일반적 RNN에서 time-step 진행에 따라 값이 점점 커지거나, 점점 작아져서 발생하는 exploding or vanishing gradient 문제가 해결되어 안정적 학습이 가능하다.

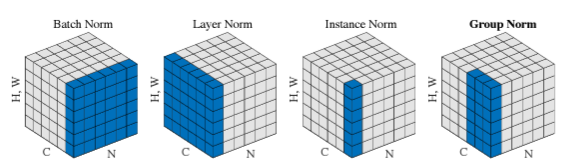
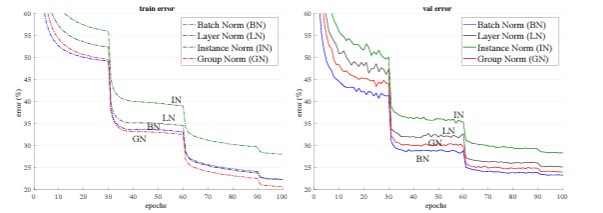
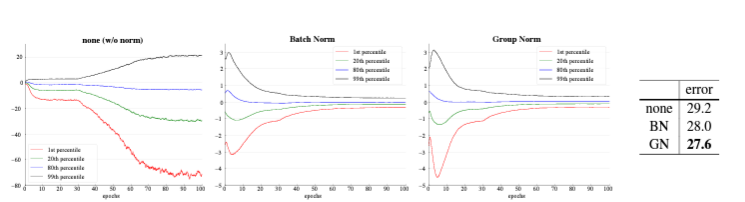
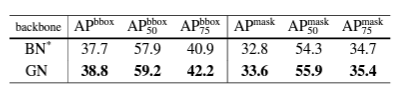
(이 이미지는 group normalization 논문에서 가져온 이미지이다. group normalization 관련된 내용은 아래 글 참조 바란다.)
2024.03.28 - [머신러닝] - Group Normalization 논문 리뷰
Group Normalization 논문 리뷰
Group Normalization 배경 설명Group Normalization은 Kaming He가 저자로 포함된 ECCV 2018년 논문이다. Computer vision 분야의 필수 component인 Batch Normalization의 한계와 그를 해결하기 위한 Group Normalization을 제시하
devhwi.tistory.com
Analysis
Invariance under weights and data transformations
- LN은 BN이나 WN(weight normalization)과 연관이 있다.
[Weight re-scaling and re-centering]
- BN과 WN은 weight vector가 a만큼 scaling 되었을 때, mean과 standard deviation은 a만큼 scaling 된다.
- scaling 전후의 normalization 값은 같기 때문에, BN과 WN은 weights의 re-scaling에 대해 불변하다.
- 하지만, LN은 single weight vector의 scaling에 따라 변한다.
- LN은 전체 weight matrix의 scaling이니나, weight matrix 모든 원소들의 shift에 대해서 불변이다.
[Data re-scaling and re-centering]
- 모든 normalization 방법들은 데이터셋의 re-scaling에 대해 불변하다.
Geometry of parameter space during learning
- 학습은 function이 같더라도 parameter에 따라 달라질 수 있다.
- 이 section에서 분석을 통해, normalization scalar σ가 implicit 하게 learning rate를 감소시키고, 학습을 더 안정적으로 만들 수 있다는 것을 확인한다.
Experimental results
- LN을 6개 RNN task에 적용해 보았다. (image-sentence ranking, QA, contextual language modeling, generative modeling, handwriting sequence generation, MNIST classification)
- LN의 기본 gain은 1, biases는 0으로 설정하였다.
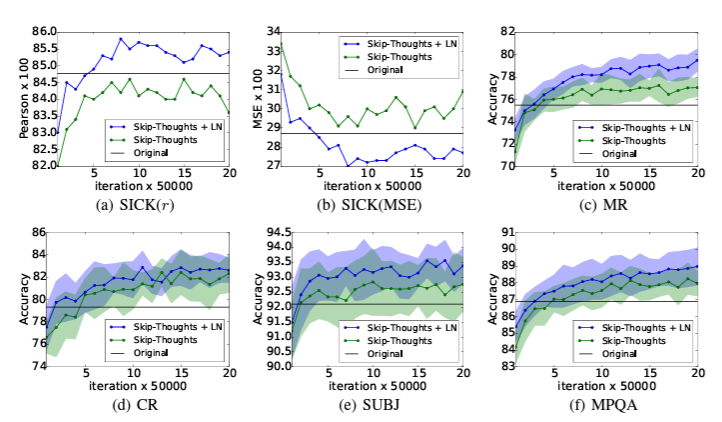
Order embeddings of images and language
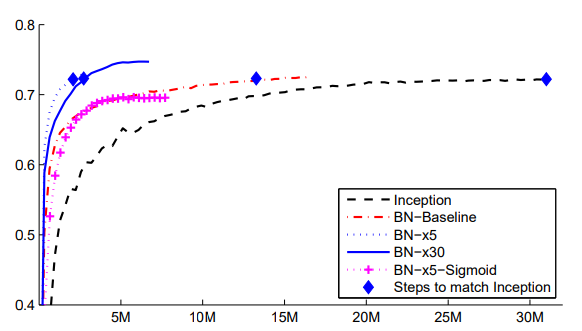
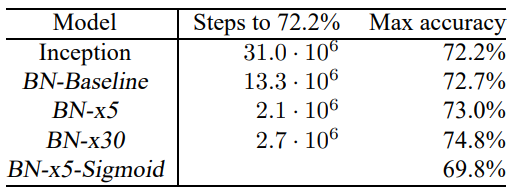
- validation curve를 보았 을때, LN의 학습속도가 매우 빠른 것을 볼 수 있다.
- 성능도 제일 좋다.
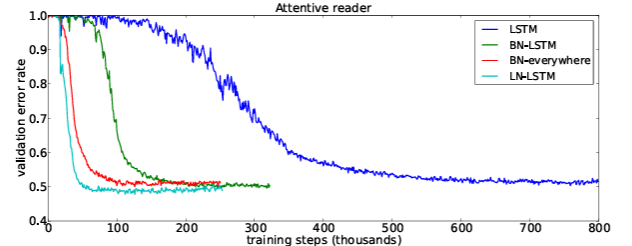
Skip-thoghts vectors
- skip-thoghts는 sentence representstions를 unsupervised로 학습하는 방법이다.
- LN을 이용하였을 때, 속도 향상뿐 아니라, 성능면에서도 이점을 주는 것을 확인할 수 있다.(표에서 십자가 표시는 한 달 학습시킨 모델이다. - 오래 학습시켰을 때)

ETC
- RNN Model에서 효과를 보았다.
- 하지만, CNN에서는 BN이 좋은 성능을 보였다. (input의 분포가 계속 바뀌기 때문에)
Reference
BA, Jimmy Lei; KIROS, Jamie Ryan; HINTON, Geoffrey E. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.
총평
- 정말 간단하고, 직관적이고, 그다음 논문(Group Normalization)을 먼저 읽은 터라 쉽게 읽혔다.
- 이런 기본적인 논문들은 아이디어가 너무 유명해져서, 논문 발표 당시 풀고자 했던 문제와 상황을 알지 못하는 경우가 많은데(논문으로 인해 이미 풀렸으므로), 당시 저자들이 어떤 생각과 문제에 집중했는지를 알게 되어, 꼭 읽어야겠다.
'머신러닝' 카테고리의 다른 글
| Group Normalization 논문 리뷰 (25) | 2024.03.28 |
|---|---|
| Batch Normalization (Accelerating DeepNetwork Training by Reducing Internal Covariate Shift) 논문 리뷰 (43) | 2023.11.10 |
| Decision Tree(의사결정나무 ) (17) | 2023.08.29 |
| t-SNE(t-distributed Stochastic Neighbor Embedding) (1) | 2023.04.26 |
| Logistic Regression(로지스틱 회귀 분석(2)-다중 분류) (1) | 2023.04.23 |