반응형
PCA는 차원 축소의 대표적인 기법이다. 다루고자 하는 데이터의 차원이 많을때, 보통 PCA를 먼저 생각하게 된다. 수업에서 배운 기억이 남아있는데, 너무 오래되어, 다시 한번 공부해보기로 한다.
PCA 란?
- PCA(Principal Component Analysis)는 이름 그대로, 데이터에서 주성분(Principal Component)을 추출하여, 주성분만으로 원 데이터를 표현하는 방법이다.
- PCA는 다차원의 데이터셋 내에서 변수들간의 상관관계를 이용하여, 이를 새로운 좌표계로 변환하여 차원을 축소한다.
- PCA는 다음과 같은 이유로 많이 사용된다.
- 데이터의 차원 축소 : 실제 데이터 분석에서 데이터의 Dimension은 고차원인 경우가 많다. 데이터의 모든 Dimension을 하나 하나 분석하기는 매우 어렵다. 이런 경우 PCA를 이용하여, 저차원으로 축소하여 분석하는 경우가 많다.
- 데이터의 잡음 제거 : PCA에서는 주성분을 추출하는 과정을 거치기 때문에, 이 과정에서 데이터의 Noise를 제거할 수 있다.
- 시각화 : PCA를 통해, 데이터를 3차원 이하로 줄이면, 데이터의 패턴이나 구조를 눈으로 확인 할 수 있다.
- 계산 효율성 : PCA를 활용하여, 저차원으로 데이터를 분석하면 계산 효율성이 크게 향상된다. 머신러닝 기법에서 데이터 전처리로 PCA를 많이 활용하는 경우도 많다.
- 데이터 분석 시, PCA를 마구 사용하는 경우가 많은데, PCA 사용 시, 다음과 같은 점을 유의해야한다.
- 해석력 감소 : PCA는 고차원의 데이터를 저차원의 새로운 축으로 다시 표현하는데, 이때 저차원에서의 각 component가 원래 데이터의 어느 요소와 연관성이 있는지 해석이 어렵다.
- 정보 손실 : 정보 손실을 최소화하는 쪽으로, 차원을 축소하지만, 이 과정에서 많은 정보가 유실된다.
PCA의 원리
- PCA의 원리를 한마디로 표현하자면, 변수들의 Covariance Matrix에서 Eigenvector와 Eigenvalue를 구한 후, 원하는 만큼의 Eigenvector만 사용하여 변수를 표현하겠다는 것이다.
- Covariance Matrix로 선형 변환한다는 것이 중요한데, 각 차원의 변수들을 다른 변수들과의 상관관계를 표현해서 나타내겠다는 의미이다.
- 예를 들어, 아래와 같이 선형 변환을 한다고하면, 선형 변환으로 구해진 새로운 변수들은 기존 변수들의 선형적 관계를 통해 구해진다. 이를 통해서, 새로운 차원의 변수는 기존 데이터의 여러 차원의 정보를 동시에 지니게 된다.
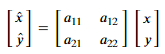
[Covariance 란?]
- Covariance는 두 변수가 함께 변화하는 정도로, 두 변수 간의 관계를 나타내는 통계값이다.
- Variance와 달리, 두 변수 간의 상관 관계를 나타내기 때문에, 방향의 개념도 포함한다. (양수 : 두 변수가 양의 상관관계, 음수: 두 변수가 음의 상관관계)

[Covariance Matrix란?]
- 다차원 변수에서 각 차원의 변수 간 Convariance를 Matrix 형태로 나타낸 것이다.
- N차원의 데이터는 N X N 형태의 Convariance Matrix로 나타나게된다.
- k X k의 대각 성분은 Variance를 의미한다.
[Eigenvector & Eigenvalue란?]
- Eigenvector는 특정 행렬이 곱해져도, 방향이 변하지 않는 벡터를 의미한다. 즉, PCA에서 Covariance Matrix를 이용해서, 선형 변환을 했을때도 방향이 변하지 않는 행렬을 의미한다.
- Eigenvalue는 Eigenvector로 선형 변환하였을때의 길이의 비율을 의미한다.
- PCA에서 Eigenvalue는 주어진 데이터셋의 주성분 중 얼마나 많은 variance를 설명할 수 있는지에 대한 수치이다. (즉, Eigenvalue가 클수록 중요한 정보를 많이 담고 있다고 해석된다.)
- N차원의 데이터에서는 N개의 Eigenvector & Eigenvalue가 나온다.
이것을 그림으로 이해해보자.
아래 그림과 같은 2차원의 데이터 분포가 있다.

해당 데이터에서 각 차원의 평균이 원점이 되는 새로운 축을 그린다. (Conviance에서 mean shift하는 과정을 의미한다.)
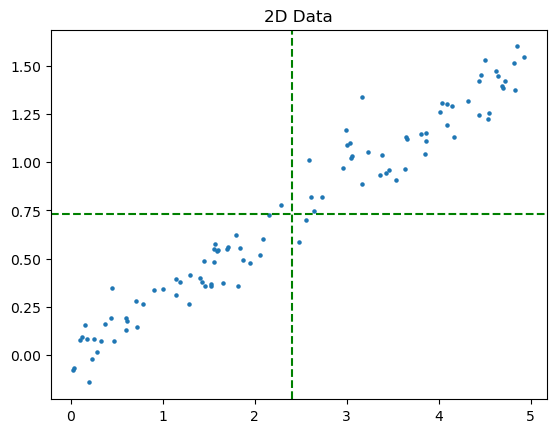
이때, 우리는 분산(새로운 원점인 기존 데이터들의 평균부터 각 데이터까지의 거리의 합)이 최대가 되는 직선을 구할 것이다.)
이 부분이 약간 헷갈릴 수 있는데, 피타고라스 정리를 생각하면 된다. 데이터를 새로운 축에서 가장 잘 표현하기 위해서는 기존 데이터와 새로운 축에서의 데이터 간의 거리가 가장 작은 선을 축으로 삼아야한다.)
아래의 그림에서 c는 데이터 포인트와 평균 간의 거리기 때문에 고정이다. 피타고라스 정리에 의해서 c가 고정되어 있을때, b(원 데이터와의 거리)가 최소인 값을 구하려면 a가 최대가 되어야한다.
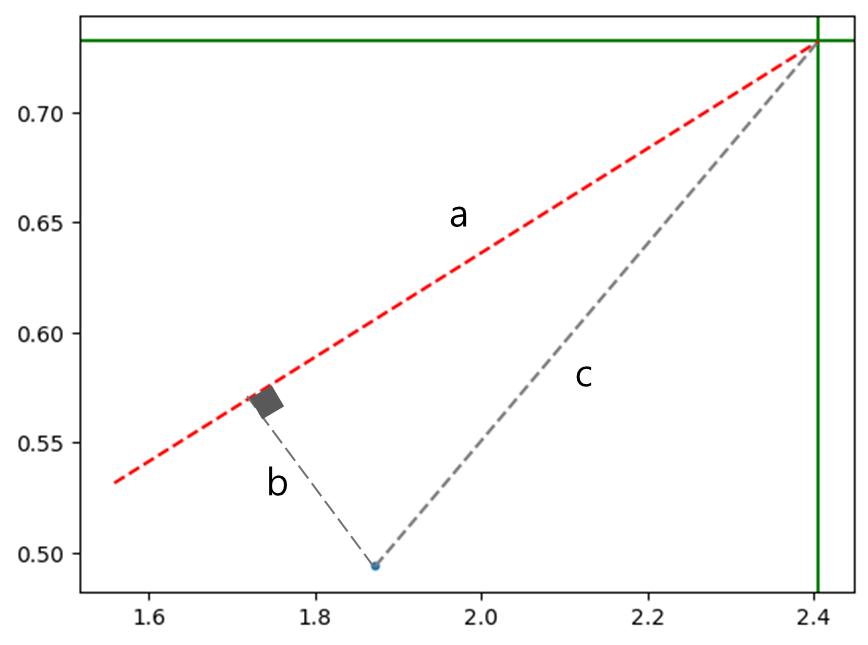
이때, a가 최대가 되는 선은, 분산이 최대가 최대가 되는 선으로 Eigenvector이다.

첫번째 구한 Eigenvector와 수직인 직선을 구하면, 두번째 Eigenvector가 된다.

PCA 파이썬 구현
- PCA는 파이썬의 scikit-learn을 통해 쉽게 사용 가능하다.
- PCA 수행 시, n_components에 몇번째 차원까지의 주성분을 사용할지를 결정한다.
import numpy as np
from sklearn.decomposition import PCA
if __name__ == '__main__':
# 2차원 랜덤 데이터 생성
np.random.seed(1)
x = 5*np.random.rand(100, 2)
# 첫 번째 특성에 대해 랜덤한 선형적 상관관계 부여
X[:, 1] = 0.3 * X[:, 0] + 0.1 * np.random.randn(100)
# PCA 모델 생성
pca = PCA(n_components=1)
# PCA 모델 학습
pca.fit(X)
# PCA 수행
transformed_data = pca.transform(X)
# 차원 변화 확인
print(transformed_data.shape)
# 주성분 확인
print(pca.components_)- Covariance Matrix와 Eigenvalue, Eigenvector를 사용하기 위해서는 numpy에 내장되어 있는 함수들을 사용하면 된다.
import numpy as np
if __name__ == '__main__':
# 2차원 랜덤 데이터 생성
np.random.seed(1)
x = 5*np.random.rand(100, 2)
# 첫 번째 특성에 대해 랜덤한 선형적 상관관계 부여
X[:, 1] = 0.3 * X[:, 0] + 0.1 * np.random.randn(100)
# Covariance Matrix 구하기
cov_mat = np.cov(X.T)
print(cov_mat)
# Eigenvalue & Eigenvector 구하기
eigenvalue, eigenvector = np.linalg.eig(cov_mat)
print(eigenvalue, eigenvector)
# 차원 변화 확인 (데이터 변환된 값)
transformed_data = eigenvector.T.dot((X - X.mean()).T).T
n_component = 1
pca_data = transformed_data[:,:n_component]
print(pca_data.shape)'Data Science' 카테고리의 다른 글
| 벡터 DB 검색 기본 개념 : Embedding (2) (1) | 2025.12.09 |
|---|---|
| 벡터 DB 검색 기본 개념 : Embedding, ANN 개요 (1) (1) | 2025.12.08 |
| DTW(Dynamic Time Warping) (1) | 2023.06.02 |
| 이상치(Outlier) 제거 방법(2) - 머신 러닝 이용 방법 (1) | 2023.03.31 |
| 이상치(Outlier) 제거 방법(1) - 통계적 방법 (5) | 2023.03.19 |



