반응형
DTW는 두 시계열의 데이터를 비교하기 위해 자주 사용하는 방법이다. 그 원리와 사용법을 제대로 알아보자.
DTW 란?
- DTW(Dynamic Time Warping)은 시계열 데이터 간의 유사성을 비교하기 위한 알고리즘이다.
- DTW는 시계열 데이터 간의 길이나 속도가 달라도, 이것을 고려하여 유사성을 측정할 수 있기 때문에 시계열 데이터 분석에 많이 활용된다.
- DTW는 시계열 형태의 sequence 데이터에 모두 활용할 수 있다.
- DTW의 유사도를 바탕으로 두 시계열 데이터 간의 시간 정렬(time alignment)을 할 수 있다.
- DTW는 음성인식이나 자연어처리에 자주 활용된다.
DTW 이해
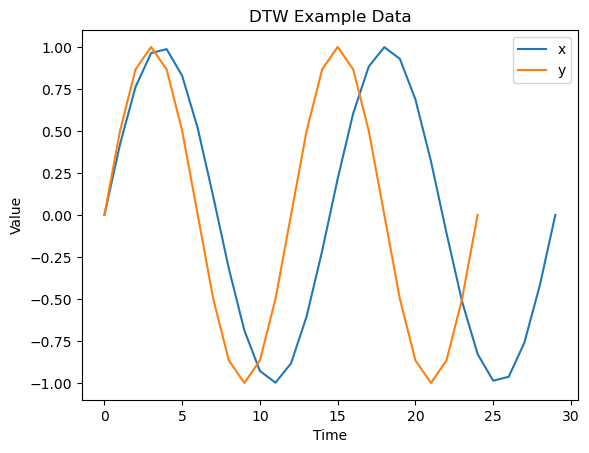
- 그림의 두 시계열 데이터를 보았을때, 길이와 형태가 다르지만, 비슷한 Pattern을 띄고 있다는 것을 알 수 있다.
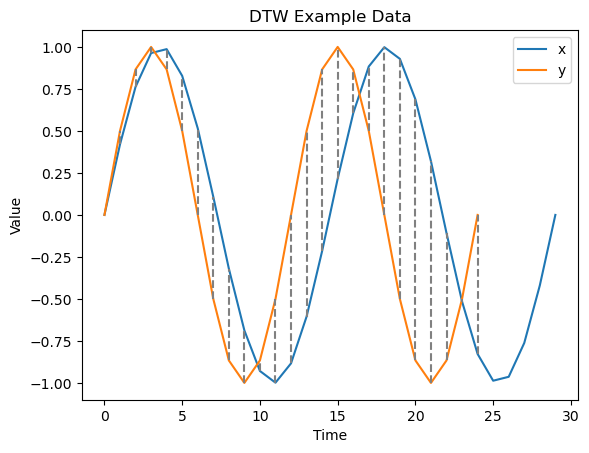
- 일반적으로 두 시계열 데이터를 비교하는 방법은 동일 시점에서 두 데이터의 값을 비교하는 것이다. 하지만, 비슷한 Pattern을 가진 두 시계열 데이터도 같은 시점에서 비교하였을 때는 큰 차이가 날 수도 있다. 특정 시점에서의 두 데이터의 값이 중요한 분석일 때는 이러한 방식이 맞지만, 두 시계열 데이터 간의 Pattern의 Similarity가 중요한 분석에서는 다른 방법이 필요하다. DTW는 한 시계열 데이터의 첫 시점에서부터 순차적으로 다른 시계열 데이터 내의 시점 데이터 중 가장 비슷한 시점을 찾고, 이 최소 거리들을 누적하여 유사도를 측정한다. 이로 인해, 길이와 시점의 차이가 있는 시계열 데이터도 유사도를 비교할 수 있다.
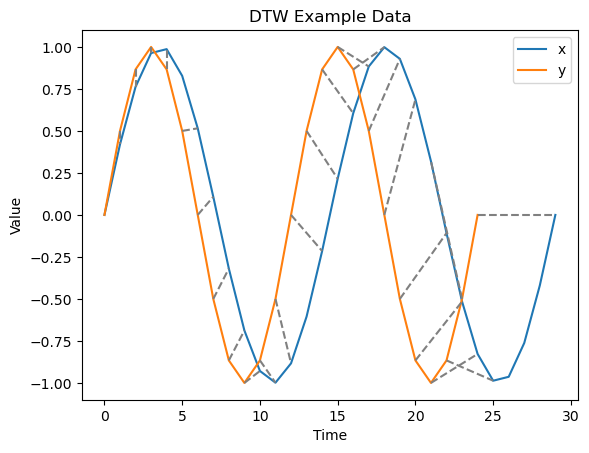
DTW 원리
- DTW는 기본적으로 다이나믹 프로그래밍 기법(문제를 여러 개의 하위 문제로 분할에서 최적해를 계산하는 방법)을 이용한다.
- DTW를 위해 우선 두 시계열의 시점간의 유사도를 측정하기 위한 거리함수를 정의해야 한다. 일반적으로 Euclidean distance가 많이 활용된다.
- DTW에서 시점을 탐색에서는 다음의 조건을 충족시켜야한다.
- boundary condition : Warping 거리의 첫 번째와 마지막은 이어져야 한다.
- continuity : Warping 경로는 대각 요소를 포함한 인접한 셀로 제한된다.
- monotonicity: Warping 경로는 음의 방향으로 이동하지 않는다. (이미 matching된 warping이면, 이전 시점은 보지 않는다.)
- DTW는 위의 조건들을 만족하면서 Warping 거리의 합이 최소가 되는 경로를 찾는 과정이다.
- Warping 거리의 합은 아래 수식으로 나타난다.
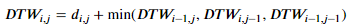
이를 그림으로 표현하면 DTW를 구하는 방식은 아래와 같다. (편의를 위해 맨해튼 거리를 이용한다.)
우선 boundary condition에 의해 Warping 거리의 첫번째와 마지막은 이어져야한다. 따라서, Warping 경로가 빨간색 표시된 두 점은 무조건 지나가야 한다. 맨 끝 시점(맨 오른쪽 위 빨간 1)에서 인접한 값들을 보았을 때, 가장 distance가 작은 쪽은 왼쪽에 위치한 1이다.
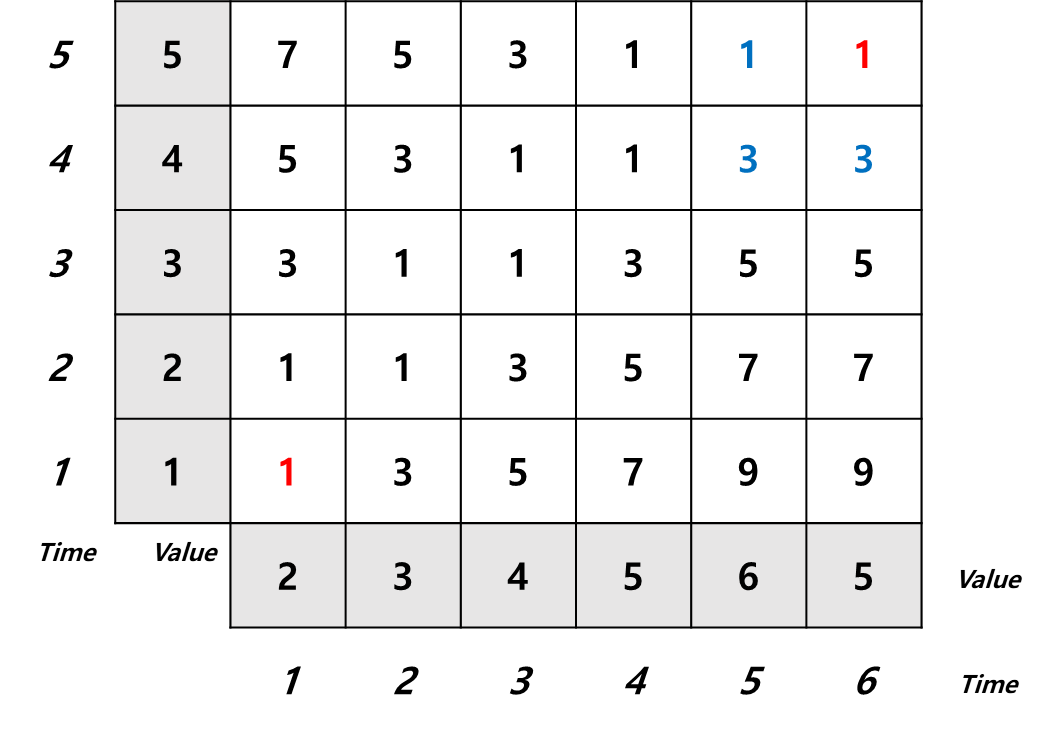
전 단계에서 찾은 1에서 인접한 값들을 보았을때, (monotonicity 조건에 의해 matching 된 값들을 넘어서는 값에서는 찾을 수 없다. → 찾는 방향은 거꾸로 진행했기 때문에 앞선 설명과 헷갈릴 수 있다.) 왼쪽에 위치한 1과 대각선에 위치한 1이 후보가 된다. 두 값 중, 어느 값을 선택해도 상관없지만, 일반적으로 대각선을 많이 선택한다.

이 과정을 반복하면, 아래와 같은 경로가 완성된다.

경로를 따라 distance들을 모두 합하면, DTW가 계산된다.
DTW 값은 (1+1+1+1+1+1) = 6
DTW 코드 구현
DTW의 구현은 Dynamic Programming을 그대로 구현하면 된다.
import numpy as np
def dtw_distance(x, y, dist):
m = len(x)
n = len(y)
# DTW 행렬 초기화
dtw = np.zeros((m+1, n+1))
# 첫 번째 행 초기화 (경로 시 제외하기 위해)
dtw[0, 1:] = np.inf
# 첫 번째 열 초기화 (경로 시 제외하기 위해)
dtw[1:, 0] = np.inf
# DTW 행렬 계산
for i in range(1, m+1):
for j in range(1, n+1):
cost = dist(x[i-1], y[j-1]) # 두 데이터 포인트 간의 거리 또는 유사성 계산
dtw[i, j] = cost + min(dtw[i-1, j], dtw[i, j-1], dtw[i-1, j-1])
# DTW 거리 반환
return dtw[m, n]
def distance(a, b):
return abs(a - b)
if __name__ == '__main__':
# 예시 시계열 데이터
x = [1, 2, 3, 4, 5]
y = [2, 3, 4, 5, 6, 7]
dtw_distance = dtw_distance(x, y, distance)
print("DTW 거리:", dtw_distance)'Data Science' 카테고리의 다른 글
| 벡터 DB 검색 기본 개념 : Embedding (2) (1) | 2025.12.09 |
|---|---|
| 벡터 DB 검색 기본 개념 : Embedding, ANN 개요 (1) (1) | 2025.12.08 |
| PCA(Principal Component Analysis) (1) | 2023.05.04 |
| 이상치(Outlier) 제거 방법(2) - 머신 러닝 이용 방법 (1) | 2023.03.31 |
| 이상치(Outlier) 제거 방법(1) - 통계적 방법 (5) | 2023.03.19 |



