반응형
BitNet 배경 설명
- BitNet은 Microsoft와 칭화대학교에서 23년 10월에 제출한 논문이다.
- 커뮤니티에서 해당 논문에 대해 우연히 접하게 되어 리뷰를 하게 되었다.
- LLM은 성능 향상을 위해 model의 parameter를 키우는 방향으로 성장하고 있다.
- Parameter가 늘어나면서, model의 성능은 점점 좋아지지만, 1) model 자체의 용량이 커지면서 필요한 storage 용량의 증가 2) 연산을 위해 필요한 memory의 증가 3) 프로세서의 연산 속도 한계 등의 H/W의 제약이 대두되었다.
- 특히, mobile phone과 같은 제한된 resource 내에서 on-device LLM 동작을 위해서는 단순히 H/W의 spec을 늘리는 방향으로 model parameter의 증가세를 따라갈 수 없게 되었다.
- 예를 들어, 136B의 parameter 크기를 가지는 GPT-3의 경우 용량을 줄이기 위해, 16bit 연산을 진행함에도 불구하고, 약 272GB의 어마어마한 parameter 용량을 가지게 된다.(심지어, GPT-3는 최신 LLM에 비해 parameter가 많은 것도 아니다.) 이러한 parameter를 on-device 내에서 올리기는 매우 어렵다.
- AI 분야에서의 weight 연산은 그 자체의 정밀도에 크게 민감하지 않기 때문에, 연산의 정밀도를 내주면서도, parameter의 bit를 줄여가는 방식으로 발전하고 있다. (4bit uint 연산으로 대체 등)
- 이 논문도 이러한 LLM의 방향성 속에서 극단적으로 Transformer의 연산을 1bit로 진행하고자 하는 시도이다.

Abstract
- LLM의 parameter 크기가 커지면서, 에너지 낭비로 인한 환경 문제가 대두되고 있다.
- 이 논문은 BitNet이라는 확장가능하고, 안정적인 1-bit Transformer 구조를 소개한다.
- 특히, 기존 Fully-Connected Layer를 대체할 수 있는 1-bit weight의 BitLeanear를 소개한다.
- 실험에서 BitNet은 8-bit 방식이나, 16-bit 방식의 Transformer에 필적할만한 성능을 보이면서, 매우 큰 메모리&에너지 절감을 이뤘다.
- 또한, BitNet은 일반적 32-bit Transformer와 유사한 성능 Scaling 법칙을 따라서, Language model의 parameter 크기를 늘리는 트렌드에 더 효과적인 방안으로 사용될 가능성이 있다.
Introduction
[배경]
- 최근 LLM은 빠른 성장을 이뤘지만, LLM의 높은 inference cost와 에너지 사용은 감당하기 어렵다.
- model의 크기가 커질수록, model parameter를 처리하기 위한 memory bandwidth가 bottleneck이 되어, inference 성능이 제한되기도 한다.
- 특히, 이런 모델을 분산 시스템이나, 멀티 디바이스 환경에 배포할 때, 디바이스 간 communication overhead(주로 N/W IO)의 영향이 커져, inference latency와 에너지 소비를 유발한다.
- Model quantization은 이런 문제를 해결하기 위해, 등장했고, 성능을 유지하면서 memory와 연산량을 줄이는 데 성공하였다.
[quantization 연구들 - post training]
- 현재 존재하는 대부분의 quantization 방법은 post-training 방식이다. (기존 모델로 학습 후, quantization 방식으로 이를 reference로 retraining)
- 하지만, 정밀도가 더 낮아지면, model은 quantization을 위해 최적화되지 않았기 때문에, 정확도의 큰 손실이 생긴다.
[ quantization 연구들 - quantization aware training ]
- 또 다른 방법으로는 quantization-aware training 방법이 있는데, post-training과 비교하여 일반적으로 더 높은 성능을 보인다.
- 이 방법은 모델을 계속해서 훈련과 fine-tuning이 가능하다.
- quantization-aware training의 주요 문제는 최적화에 있다. 즉, 정밀도가 낮아질수록, 최적화가 어렵다는 것이다.
- 또한, 이 방법이 LLM의 scaling 법칙(parameter가 커질수록 성능이 좋아진다.)을 따르는지 미지수이다.
[논문 소개]
- 이 논문에서는 LLM에 binarization(극단의 quantization) 적용에 초점을 맞춘다.
- 앞선 연구들은 주로 CNN에 초점을 맞췄고, 최근 들어 몇 개의 binarized Transformer가 등장하기 시작했다.
- 하지만, 이런 연구들은 LLM과 꽤 다른 기계번역이나, BERT pretraining에 초점을 맞췄다. (예를 들어, 기계번역은 encoder-decoder 구조를 사용, BERT pretraining은 bidrectional encoder를 사용)
- 이 논문은 최초의 1-bit large language model에 quantization-aware training을 도입한 최초의 연구이다.
- 이 논문에서는 BitNet이라는 LLM의 memory와 연산을 효율화하여, LLM에 사용할 수 있는 1-bit Transformer 구조를 제시한다.
- BitNet은 low-precision binary weights와 quantized activations를 사용하였다.
- BitNet의 구현은 단순히 Transformer의 linear projection을 대체하면 되기 때문에 매우 간단하다.
[실험 결과]
- SOTA quantization 방법들이나, 16-bit Transformer들과 비교해 보았을 때, BitNet은 memory와 에너지 사용을 매우 절감하면서도 preplexity와 downstream task 정확도에서 그들과 비견할만한 좋은 성능을 보였다.
BitNet
- 아래 그림과 같이 BiTNet은 Transformer의 self-attention, feed-forward를 쌓는 구조와 비슷한 형태를 가진다.
- BitNet은 BitLinear라는 연산을 기존 matrix multiplication 대신 사용한다. 이 연산은 1-bit의 model weights를 가진다.
- BitNet에서는 BitLinear를 제외한 다른 연산들은 8-biit의 값을 사용하는데, 그 이유는 다음과 같다.
- residual connections과 layer normalization은 LLM 연산에 비해 매우 미미한 cost만 사용한다.
- 모델의 커질수록 QKV 변환의 연산이 parametic projection보다 훨씬 작다.
- samling 수행을 위해, high-precision probability를 사용해야하기 때문에, 입, 출력 임베딩 정밀도 보존한다.

BitLinear
- 먼저 weight를 +1, -1 양값이 나오는 signum function을 통해, binarize한다.
- 표현 가능한 capacity를 늘리기 위해, binarization 전에 weights를 mean 0 값으로 centralize 해준다.
- scaling factor를 이용하여, binarization 이후에 실제 값과, binarized weight의 l2 error를 줄인다.
- weight의 binarization은 아래 식과 같이 표현된다.

- 이후, activation을 b-bit precision으로 quantize 한다. 이때, 아래와 같이 absmax quantization 방법을 사용하였다.
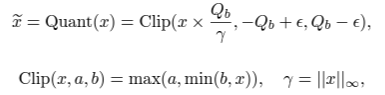
- non-linear function(activation function) 전에 모든 값에 minimum을 빼줘서, 모두 양수 값으로 만든다.

- 위의 quantization function을 이용하여, matrix multiplication은 다음과 같이 구해진다.

- W와 x의 mutually independent와 같은 분포를 공유한다는 것을 가정하면, y의 variance는 아래와 같이 구할 수 있다.

- quantization 후, 분산 보존을 위해, activation quantization 전에 LayerNorm을 사용한다. 이렇게 하면, output y는 Var(y) ≈ E [LN(x)^2] = 1과 같이 구해진다.
- Transformer에서 이것은 SubLN과 정확히 같은 구현을 가진다.
- SubLN과 앞선 quantization 방법을 이용하여, BitLinear를 다음과 같이 정의한다.
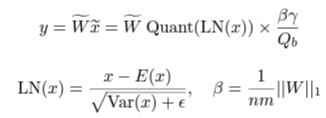
[Model parallelism with Group Quantization and Normalization]
- LLM의 핵심요소 중 하나는 여러 device에서 matrix multiplication을 분산처리하는 model parallelism이다.
- 이 model parallelism의 전제 조건은 tensor들이 partition dimension으로는 각기 independent 하다는 것이다.
- 하지만, 모든 parameter들은 전체 tensor들로부터 계산되기 때문에, 그 전제 자체가 깨진다.
- 이를 해결하기 위한 방법으로 각 parameter에 all-reduce operation을 제안한다.
- 각 parameter들 간의 communication은 적더라도, model이 깊어질수록, 전체 synchronization 크기는 커지고, 이로 인해 forward-pass는 느려진다.
- SubLN에서도 이 문제는 발생하는데, mean과 variance가 partition 방향으로 구해져야 하기 때문이다.
- 이를 해결하기 위해, 이 논문에서는 model parallelism을 효율적으로 구현하는 매우 간단한 방법을 소개한다. 우선, weights와 activations들을 그룹으로 나누고, 각 그룹의 parameter를 독립적으로 추정한다. 이런 방법을 이용하면, 각 parameter들은 별도의 communication 없이 locally 하게 연산이 된다.
- 이 방법을 "Group Quantization"이라고 명명하고 다음과 같이 정의한다.
- weight matrix W(n X m)에 대해, partition 방향으로 G개의 group으로 나눈다. 각 group은 n/G X m의 size를 가진다. 그리고, 각 group은 독립적으로 parameter를 추정한다.

- 비슷하게, 각 group에 대한 activation을 구한다.

- LN을 위해, group normalization을 적용하는데, 이때 mean과 variance는 각 group에 독립적으로 구하여 사용한다.

- 이 방법으로, 효율적인 Group Qunatization과 Normalization을 이용한 model parallelism이 가능해졌다.
Model Training
[Straight-through estimator]
- 1-bit model 학습을 위해, straight-through estimator(STE)를 이용하여 backpropagation 간 gradient approximatin에 사용했다.
- 이 방법은 backward pass에서 미분 불가능한 연산(Sign, Clip 등)을 bypass 하는 것이다.
- STE는 gradient가 미분 불가능한 연산에 대한 영향 없이 model의 학습을 돕는다.
[Mixed precision training]
- weights와 activations가 quantized 되어 precision이 떨어졌지만, gradient와 optimizer는 high precision을 유지하고 있어 안정적인 학습과 정확도를 유지한다.
- 기존 연구를 따라, parameter update를 위한 latent weight를 high precision으로 유지한다.
- latent weights는 forward pass 단에서 binarized 될 것이고, inference process에서는 사용되지 않는다.
[Large learning rate]
- optimization 단에서 1-bit weight 상에서 거의 차이가 나지 않는 small update가 종종 일어난다.
- 이 현상이 training 초기 단에서 일어나면, 그 문제는 더 심각해진다. (초기단에서는 빠른 converge가 필요하기 때문에)
- 이 문제를 해결하기 위해, 여러 방법들을 사용하였는데, 그중 하나가 빠른 optimization을 위해 learning rate를 키우는 것이다.
- 저자들은 BitNet이 초반 큰 learning rate를 사용했을 때 convergence 측면에서 큰 이득을 보는 것을 확인했다.
Computational Efficiency
- 가장 중요한, BitNet의 computational 효율성을 energy 측면과 memory 측면에서 확인해 봤다.
- 특히, LLM의 꽃인 matrix multiplication을 중점적으로 확인했다.
[Arithmetic operation energy]
- 기존 연구에 따르면, 기존 산술 연산에서 bit 수에 따른 에너지 소모는 다음과 같이 알려져 있다.
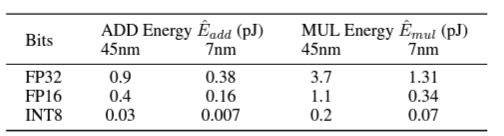
- 기존 Transformer에서 m X n과 n X p의 matrix multiplication 연산의 energy 소비는 아래와 같이 계산된다.
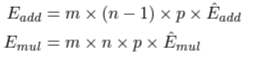
- BitNet에서는 matrix multiplication의 주요 연산이 addition operation이다. (weight가 1bit이므로) BitNet에서 energy 소모는 다음과 같이 계산된다.

- 이것은 energy 소비 측면에서 기존 Transformer에 비해 매우 적고, 특히 W1 A8(weight는 1bit, add는 8bit) 구조는 32-32, 16,16 Transformer에 비해 매우 적게 에너지가 소모된다.
→ multiplication 연산은 add 연산에 비해 cost가 매우 크기 때문에, 많은 compiler들이 multiplication을 add로 바꾸는 방법으로 연산을 optimize 하곤 한다. weight에 1bit를 할당해 줘서, multiplication 연산을 add 연산으로 바꾸는 효과를 볼 수 있는 것이다.
FP16 Transformer와의 비교
Setup
- BitNet 모델을 다양한 size의 language model에서 비교하기 위해, parameter의 size를 125M에서 30B까지 영역에서 비교해 보았다.
- model은 English-language corpus(Pile, Common Crawl, RealNews, CC-Stories)를 통해 학습되었고, Sentencpiece tokenizeer로 전처리하였고, vocabulary size는 16K이다. 비교를 위한 Transformer도 동일하게 처리하였다.
Inference-Optimal Scaling Law
- 기존 연구에 따르면, Transformer는 연산 cost에 따른 loss는 power law를 따른다. (연산량에 제곱에 비례하게 low가 줄어든다.)
- 1-Bit BitNet도 이를 따르는지 확인해 보았는데, 결과적으로 BitNet도 어느 정도 power law를 따름을 보인다.
- 하지만, 실제 연산 cost와 loss의 관계를 적절히 modeling 하지 못하는데, 기존 연구들은 FLOP을 계산하여 계산량을 추정하였지만, BitNet은 정수 계산이 우세하기 때문에 적용되지 않고, 기존 연구들의 추정은 추론보다는 학습 계산량 추정에 불과하였기 때문이다.
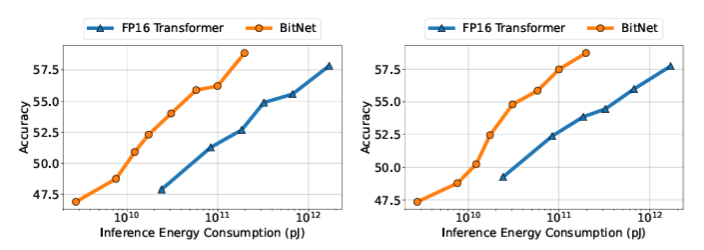
- 이 연구에서는 LLM의 효율성을 더 잘 이해하기 위해, inference 단에서 energy 소비와 loss 간의 관계를 모델링하는 Inference-Optimal Scaling Law(아래 왼쪽 그래프)를 소개한다.
- Inference-Optimal Scaling Law를 통해, BitNet이 기존 FP16 Transformer에 비해 훨씬 더 높은 scaling 효율성을 가지고 있음을 확인할 수 있다. 또한, FP16 model과 동일한 성능을 얻기 위해 사용되는 energy의 소모량은 매우 적다.

Downstream Task들에서의 비교
- loss 뿐 아니라, BitNet의 효과성을 확인하기 위해, loss에 비해 더 어려운 capacity를 측정해 본다.
- 0-shot과 4-Shot의 downstream task들에서 test를 진행한다.
- loss scaling curve와 비슷하게 downstream task는 computation cost가 증가하면 performance가 증가한다.
Stability Test
- low-bit Transformer의 가장 큰 어려움은 optimization 단에서의 안정성이다.
- 따라서, 저자들은 BitNet과 FP16 baseline의 peak learning rate를 바꿔가면서 실험하여, stability test를 진행하였다.
- 아래 그래프에서 보듯, BitNet은 FP16에서 불가한 큰 learning rate에서 converge가 가능하였고, 이것은 학습 단에서의 BitNet의 안정성을 증명한다.
- 이것은 optimization을 큰 learning rate로 진행하여, 빠른 학습이 가능함을 보인다.

Post-training Quantization과 비교
Setup
- BitNet과 SOTA quantization 방법들을 비교했다.
- 이러한 방법들은 FP16 Transformer model에 대한 post-training을 진행하는 방법들이다. 이러한 방식들은 weight와 activation의 precision을 모두 줄인 경우(Absmax, SmoothQuant)와 weight만 줄인 경우(GPTQ, QuIP) 들로 나뉘는데, 이들과 비교하기 위해 weight-only quantization에는 W4 A16, W2A16을, weight-and-activation quantization에는 W8 A8, W4 A4, W1A8을 이용하였다.
Result
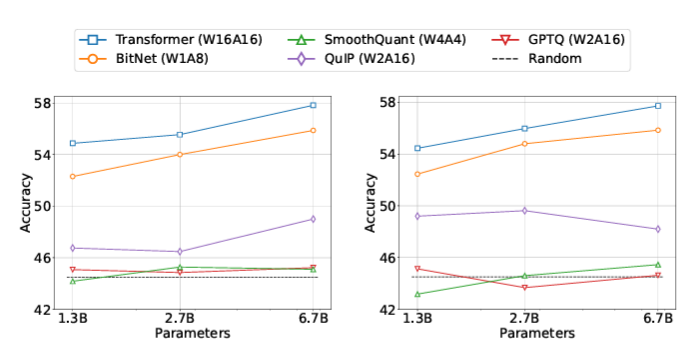
- 아래 그래프와 표를 통해, 다른 quantization 방법들과의 성능 비교 결과를 확인할 수 있다.
- 공정한 비교를 위해, 모든 model의 parameter size는 6.7B로 통일했다.
- 결과를 통해, BitNet이 lower bit를 가지고 있음에도 불구하고, 다른 quantization model에 필적할만한 좋은 성능을 보임을 확인할 수 있다.
- zero-shot score에서 BitNet은 inference cost가 훨씬 낮지만, 8bit 연산과 비교될만한 높은 성능을 냄을 확인할 수 있다.
- BitNet은 1bit model이지만, weight-and-activation quantization과 weight-only quantization에서 다른 model에 비해 좋은 성능을 보임을 확인할 수 있다.

Reference
WANG, Hongyu, et al. Bitnet: Scaling 1-bit transformers for large language models. arXiv preprint arXiv:2310.11453, 2023.
총평
- 최근, 회사에서 좋은 기회로 computer architecture 교육을 듣고 있어서, 산술 연산의 cost에 대해 관심이 많았는데, 이런 논문을 읽게 되어, 더 재밌게 읽은 것 같다.
- 실제로 강의를 진행해주시는 교수님께서 matrix multiplication 연산의 비효율성에 대해서 열심히 설명해 줘서 그런지 이 논문의 필요성에 대해 더 공감하게 되었다.
- LLM의 용량이 더 줄어서, on-device AI가 더 활발해지는 세상이 왔으면 좋겠다.
'NLP 논문' 카테고리의 다른 글
| GQA: Training Generalized Multi-Query Transformer Models fromMulti-Head Checkpoints 논문 리뷰 (33) | 2024.08.01 |
|---|---|
| LoRA: Low-Rank Adaptation of Large Language Models 논문 리뷰 (27) | 2024.07.30 |
| LLaVA: Vision Instruction Turing 논문 리뷰 (41) | 2023.10.15 |
| InstructGPT (Training language models to follow instructions with human feedback) 논문 리뷰 (1) | 2023.07.01 |
| PaLM(Scaling Language Modeling with Pathways) 논문 리뷰 (1) | 2023.06.29 |



